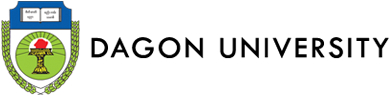Dr.Aye Aye Yu
ဒေါက်တာ ဒေါ်အေးအေးယု
Position : Professor (Head)
Degree : MSc, Ph.D (Mathematics)
Mathematics
Position : Professor
Degree : BSc honors, MSc, Ph.D (Mathematics) Position : Professor
Degree : BSc (hons;), MSc, Ph.D (Mathematics)Dr.Myo Myo Hla ဒေါက်တာ ဒေါ်မျိုးမျိုးလှDr.Khin Myo Aye ဒေါက်တာ ဒေါ်ခင်မျိုးအေး
Teacher list
| Sr.No | Department | Name | Position | Education | Thesis Title | Field Of Specialization | Current Research Project | Email/Gmail |
| 1 | Mathematics | Dr.Aye Aye Yu | Professor (Head) | Ph.D | Oscillatory Solutions Of Hyperbolic Conservation Laws | Differential Equations | (1) Boundary Stabilization of a Coupled Burgers’ PDE-ODE System (2)Stabilization of Coupled Distributed Parameter Systems |
[email protected] |
| 2 | Mathematics | Dr.Myo Myo Hla | Professor | Ph.D | Extension of QB-rings | Algebra | – | [email protected] |
| 3 | Mathematics | Dr.Khin Myo Aye | Professor | Ph.D | Numerical Methods for Transient Semiconductor Device Equations | Differential Equations | – | [email protected] |
| 4 | Mathematics | Dr. Khin Win Maw | Associate Professor | Ph.D | Fuzzy Graphs And Their Complements | Graphs Theory | – | [email protected] |
| 5 | Mathematics | Dr. Khin Thit Thit Tin | Associate Professor | Ph.D | Viscous Incompressible Flow Between Two Coaxial Rotating Porous Cylinders | Hydromechanic | – | [email protected] |
| 6 | Mathematics | U Thet Lwin | Associate Professor | M.Sc | Applied Mathematics | – | [email protected] | |
| 7 | Mathematics | Daw Myint Myint Khine | Associate Professor | M.Sc | Ordinary Mathematics | – | [email protected] |
|
| 8 | Mathematics | Daw Aye Hlaing | Lecturer | M.Sc | Convergence of Convex Sets And of Solutions of Variational Inequalities | Pure Mathematics | – | [email protected] |
| 9 | Mathematics | Daw Sandar Lwin | Lecturer | M.Sc | Parametric Interval Estimation | Social Applied | – | [email protected] |
| 10 | Mathematics | Daw Sandar Myint | Lecturer | M.Sc | Ordinary Mathematics | – | [email protected] |
|
| 11 | Mathematics | Daw San San Tint | Lecturer | M.Sc | Differential Equations | – | [email protected] |
|
| 12 | Mathematics | Daw Pyae Pyae Phyo | Lecturer | M.Sc | Engineering Mathematics | – | [email protected] | |
| 13 | Mathematics | Daw Pan Zar Phyu | Lecturer | M.Sc | Pure Mathematics | – | [email protected] |
|
| 14 | Mathematics | Dr. Aye Aye Khaing | Lecturer | Ph.D | A Study on Some General Mappings | Analysis | – | [email protected] |
| 15 | Mathematics | Dr. Wah Wah Myint Oo | Lecturer | Ph.D | Spanning Trees with a Bounded Number of Leaves in a Quasi Claw-free Graph | Graph Theory | – | [email protected] |
| 16 | Mathematics | Dr. Thwe Thwe Aung | Lecturer | Ph.D | Investigation On Integral Domains Whose Simple Overrings Have A Specified Property | Algebra | – | [email protected] |
| 17 | Mathematics | Dr. Hnin Ye Khaing | Lecturer | Ph.D | Time Dependent Drift-Diffusion Model for Semiconductors | Differential Equations | – | [email protected] |
| 18 | Mathematics | Daw Yupar Phyo | Lecturer | M.Sc | Numerical Solutions Of Initial-Value Problems For Ordinary Differential Equations | Differential Equations | – | [email protected] |
| 19 | Mathematics | Dr. Aye Aye Than | Assistant Lecturer | Ph.D | Control of Coupled PDE Systems with Observation Delay | Differential Equations | (1) Boundary Stabilization of a Coupled Burgers’ PDE-ODE System (2)Stabilization of Coupled Distributed Parameter Systems |
[email protected] |
| 20 | Mathematics | Daw Myo Myo Aye | Assistant Lecturer | M.Res | The Binomial Tree Method to Option Pricing | Applied Mathematics | – | [email protected] |
| 21 | Mathematics | Daw Yee Yee Thin | Tutor | M.Sc | Some Method To Solve Non- Homogeneous Wave Equations | Differential Equations | – | [email protected] |
| 22 | Mathematics | Daw Hnin Thinzar Zaw | Tutor | M.Sc | Some Conjectures Involving Prime Numbers | Algebra | – | [email protected] |
| 23 | Mathematics | Daw Hnin Ei Soe Than | Tutor | M.Sc | A Study On Sequences in 2-Normed Spaces | Analysis | – | [email protected] |
| 24 | Mathematics | Daw Pa Pa Zin | Tutor | M.Res | Classical And Nonclassical Shock Waves Of Riemann Problem For Conservation Laws | Differential Equations | – | [email protected] |
| 25 | Mathematics | Daw Mu Mu Han | Tutor | M.Sc | A Study On The Tidal Waves | Differential Equations | – | [email protected] |
| 26 | Mathematics | Daw Cherry Hnin | Tutor | M.Sc | 2k Factorial Experiments With Some Applications | Analysis of Two Factors (Statistics) | – | [email protected] |
| 27 | Mathematics | Daw Min Min Than | Tutor | M.Sc | Banach Fixed Point Theorem And Some Applications | Analysis | – | [email protected] |
| 28 | Mathematics | Daw Chaw Chaw Khaing Oo | Tutor | M.Sc | A Study On Boundary Layer In Compressible Viscous Fluid | Hydrodynamics | – | [email protected] |
| 29 | Mathematics | Daw Su Mon Aung | Tutor | M.Sc | Irreducible Polynomials And Reducible Polynomials In A Ring | Algebra | – | [email protected] |
| 30 | Mathematics | Daw Ei Mon Cho | Tutor | M.Sc | A Survey Of Open Sets And Closed Sets In Topological Spaces | Analysis | – | [email protected] |
| 31 | Mathematics | Daw Su Lae Mon | Tutor | M.Sc | A Study On The Basic Partial Differential Equations And Weak Soiutions Of Elliptic Problems | Partial Differential Equations | – | [email protected] |
| 32 | Mathematics | U Kyaw Myat Maung | Tutor | M.Sc | A Study On Rectilinear Vortex Motion | Hydrodynamics | – | kyawmyatmaung1990 @gmail.com |
| 33 | Mathematics | Daw Pyone Mon Zaw | Tutor | M.Sc | A Study On Stability Of Zero Solutions | Differential Equations | – | [email protected] |
| 34 | Mathematics | Daw Thwe Thwe Htun | Tutor | M.Sc | Applications Of Conformal Mapping | Hydrodynamics | – | [email protected] |
| 35 | Mathematics | Daw Saung Yamone | Tutor | M.Sc | Solving Some Roblems Of Transport Networks | Graph | – | [email protected] |
| 36 | Mathematics | Daw Swe Swe Thet | Tutor | M.Sc | Applications Of Blasius’ Theorem In Two -Dimensional Fluid Motion | Hydrodynamics | – | [email protected] |
| 37 | Mathematics | Daw Nandar Hlaing | Tutor | M.Sc | A Study On Irreducible Ring Of Endomorphisms | Algebra | – | [email protected] |
| 38 | Mathematics | Daw May Thu Kyaw | Tutor | M.Sc | A Study On Euclidean And Factorization Domains | Algebra | – | [email protected] |
| 39 | Mathematics | Daw Khin Yee Mon | Tutor | M.Sc | Some Applications Of Convex Programming | Applied Mathematics | – | [email protected] |
| 40 | Mathematics | Daw Shun Lelt Lelt May | Tutor | M.Sc | Some Applications of Variational Methods | Differential Equations | – | [email protected] |
| 41 | Mathematics | Daw Win Win Myat | Tutor | M.Sc | Solving Partial Differential Equations in Polar Coordinates |
Differential Equations | – | [email protected] |
Programmes Offered
- B.Sc. / B.Sc. (Hons) in Mathematics
- B.Sc. (Hons) in Hydrology
- B.Sc. / B.Sc. (Hons) in Sport Science
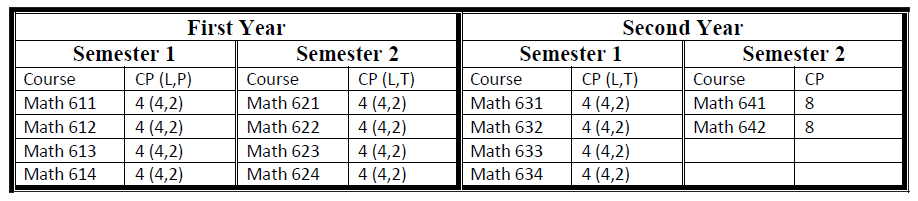
- M.Sc. and M.Res. in Mathematics
Curriculum
B.Sc. in Mathematics
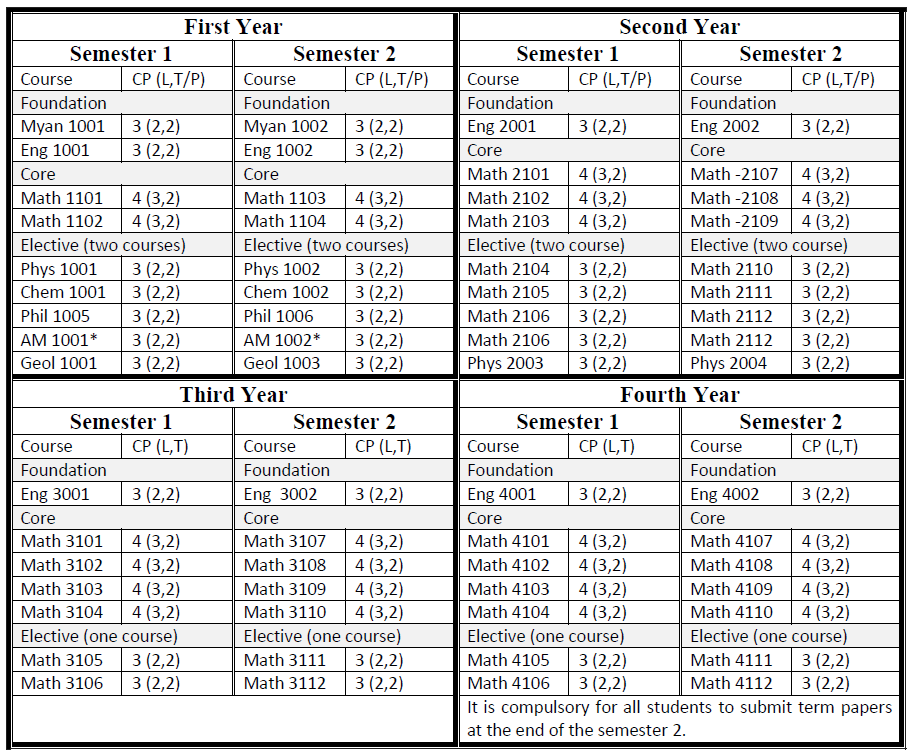
B.Sc. (Honours) in Mathematics
Students who passed second year with GPA ≥4 are eligible to attend B.Sc. (Honours) classes for three more years. After finished successfully, they are earned B.Sc. (Hons) degree majoring in Mathematics.
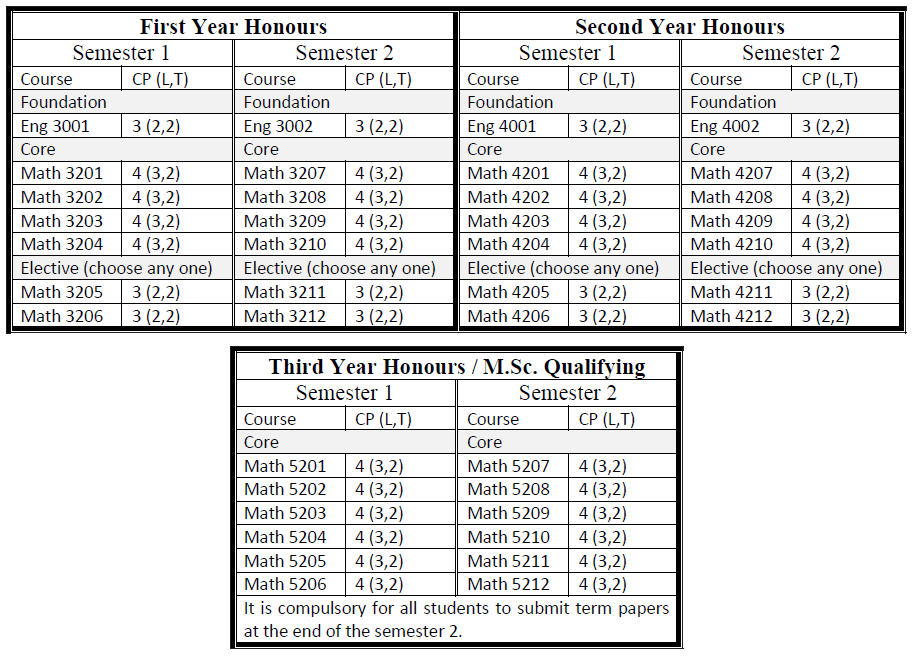
M.Sc. in Mathematics
Course Descriptions
Algebra: logic and sets, polynomial functions, permutations, combinations, binomial theorem, mathematical induction.
Analytic Geometry: lines, circles, conic sections, translation of coordinate axes, rotation of coordinate axes.
Analytic Geometry: lines, circles, conic sections, translation of coordinate axes, rotation of coordinate axes.
Trigonometry: inverse trigonometric functions
Calculus: limits, continuity exponential, logarithmic, hyperbolic functions and their inverse, differentiation of inverse trigonometric functions, differentiation of exponential, L’Hopital’s rule, Taylor series.
Calculus: limits, continuity exponential, logarithmic, hyperbolic functions and their inverse, differentiation of inverse trigonometric functions, differentiation of exponential, L’Hopital’s rule, Taylor series.
Algebra: determinants, matrices, complex numbers. Polar Coordinates System: polar coordinates, graphing in polar coordinates, areas and lengths in polar coordinates.
Analytical Solid Geometry: three dimensional Cartesian coordinate system, lines, planes, quadric surfaces.
Analytical Solid Geometry: three dimensional Cartesian coordinate system, lines, planes, quadric surfaces.
Extreme values of functions, the mean value theorem, monotonic functions and the first derivatives test, methods of integration, improper integrals, applications of integration, partial differentiation, ordinary differential equation of first order.
Analytic functions, elementary functions, integrals, residues and poles.
Functions of two or more variables, partial derivatives, directional derivatives, chain rule for partial derivatives, total differential, maxima and minima, exact differentials, derivatives of integrals, double integrals in Cartesian coordinates and polar coordinates, triple integrals in Cartesian coordinates, cylindrical coordinates and spherical coordinates, applications of multiple integrals.
Vector Algebra: dot products, cross products, triple scalar products, triple vector products.
Statics: statics of a particle, tension of a string, friction, moment and couples, centre of gravity, statics of a rigid body in a plane, jointed rods, virtual works and stability.
Statics: statics of a particle, tension of a string, friction, moment and couples, centre of gravity, statics of a rigid body in a plane, jointed rods, virtual works and stability.
Counting Methods and the Pigeonhole Principle: basic principle, permutations and combinations; algorithms for generating permutations and combinations; generalized permutations and combinations; binomial coefficients and combinatorial identities; and the pigeonhole principle.
Cardinal numbers, partially and totally ordered sets.
Spherical Trigonometry: the spherical triangle, length of small circle arc, terrestrial latitude and longitude, the fundamental formula of spherical trigonometry, the sine formula, formula C, the four parts formula, the trigonometrical ratios for small angles.
Celestial Sphere: altitude and azimuth, declination and hour angle, diagram for the southern hemisphere, circumpolar stars, the standard or geocentric celestial sphere, right ascension and declination, the earth’s orbits, celestial latitude and longitude, sidereal time, mean solar time, hour angle of a heavenly body, rising and setting, and Twilight.
Celestial Sphere: altitude and azimuth, declination and hour angle, diagram for the southern hemisphere, circumpolar stars, the standard or geocentric celestial sphere, right ascension and declination, the earth’s orbits, celestial latitude and longitude, sidereal time, mean solar time, hour angle of a heavenly body, rising and setting, and Twilight.
Vector spaces, subspaces, bases and dimensions, sums and direct sums, linear mapping, kernel and image of linear map and their dimension, and compositions of linear mapping.
Second-order linear differential equations, higher-order linear differential equations, and system of differential equations.
Vector Calculus: gradient, divergence, curl, line integrals, green’s theorem, divergence theorem, Stoke’s theorem.
Dynamics: kinematics of a particle, relative velocity, mass, momentum and force, Newton’s law of motion, work, power and energy, impulsive force, projectiles, simple harmonic motions, kinematics of a particle in two dimensions, and kinetic of a particle in two dimensions.
Dynamics: kinematics of a particle, relative velocity, mass, momentum and force, Newton’s law of motion, work, power and energy, impulsive force, projectiles, simple harmonic motions, kinematics of a particle in two dimensions, and kinetic of a particle in two dimensions.
Graph Theory: introduction, paths and cycles, Hamiltonian cycles and the traveling salesperson problem, a shortest path algorithm, representations of graphs, isomorphism of graphs, planar graphs.
Trees: introduction, terminology and characterizations of trees, spanning trees, minimal spanning trees, binary trees.
Trees: introduction, terminology and characterizations of trees, spanning trees, minimal spanning trees, binary trees.
Well-ordered sets, ordinal numbers, axiom of choice, Zorn’s lemma, well-ordering theorem.
Planetary Motions: Kepler’s three laws, Newton’s law of gravitation, the masses of the planets, the dynamical principles of orbital motion, the equation of the orbit, velocity of a planet in its orbit, components of the linear velocity perpendicular to radius vector and to the major axis, the true and eccentric anomaly expressed as a series in terms of e and the eccentric anomaly, the equation of the centre, the orbit in the space, the orbital and synodic periods of a planet, the earth’s orbit, the sun’s orbit, the moon’s orbit.
Time: sidereal time, the mean sun, the sidereal year and the tropical year, relation between mean and sidereal time, the calendar, the Julian date, the equation of time, the seasons.
Time: sidereal time, the mean sun, the sidereal year and the tropical year, relation between mean and sidereal time, the calendar, the Julian date, the equation of time, the seasons.
Elements of set theory, numerical sequences and series.
Linear maps and matrices, and determinants.
Series solutions of differential equations, special functions, and laplace transforms.
Concept of a curve, curvature and torsion, the theory of curves, and concept of a surface.
Curvilinear coordinates, and tensor analysis
Divisibility theory, congruences, Fermat’s little theorem, Euler’s generalization of FLT, Wilson’s theorem, and Eulers-function.
Continuity and differentiation
Scalar products and orthogonality, matrices and bilinear maps
Central force motion, kinematics of plane rigid bodies, kinetics of plane rigid bodies, impact, dynamics of a particle in three dimensions, dynamics of system of particles, and moment of inertia.
Introduction to probability theory, random variables, conditional probability and conditional expectation, mean, median, mode, standard deviation, correlation, and regression.
Conformal mapping and application of conformal mapping.
Primitive roots, quadratic congruence and quadratic reciprocity law, perfect numbers and Fermat’s numbers, and representation of integers as sum of squares.
Methods of mathematical research and the Riemann-Stieltjes integral.
Numerical methods in general and numerical methods in linear algebra.
Basic properties of linear programs, the simplex method, duality, dual simplex method and primal dual algorithms.
Fourier series, integrals and transforms, and partial differential equations.
Markov chains
The idea of an algorithm, pseudo code descriptions of algorithms, efficiency of algorithms, algorithms for arithmetic and algebra, coding and implementations of algorithms in some programming languages.
Sequences and series of functions
Topology of the line and plane, topological spaces, bases and sub-bases.
Semigroups, monoids and groups, homomorphisms and subgroups, cyclic groups, cosets and counting, normality, quotient groups, and homomorphisms.
Density and specific gravity, theorems on fluid-pressure under gravity, pressure of heavy fluids, thrusts on curved surfaces and floating bodies, stability of floating bodies, equation of continuity, equation of motion, and some three dimensional flows.
The exponential distribution and the Poisson process.
Formulations of integer programming, branch and bound algorithms, and cutting plane methods.
Power series, the exponential and logarithmic functions, the trigonometric functions, and Fourier series.
Continuity and topological equivalence, metric and normed spaces
Symmetric, alternating, and dihedral groups, categories, products, coproducts, and free objects, direct products and direct sums, free groups, free products, generators and relations.
Axisymmetric flow, Stoke’s stream function, some two-dimensional flows, and general motion of cylinder
Numerical methods in linear algebra, and numerical methods for differential equations.
Systems of differential equations, and linear systems with an introduction to phase space analysis.
Continuous transformations of metric spaces, Euclidean spaces, continuous functions of several real variables, partial derivatives, linear transformations and determinants, the inverse function theorem, the implicit function theorem, functional dependence.
Separation axioms, compactness, concept of product topology and examples.
Free abelian groups, finitely generated abelian groups, the Krull-Schmidt theorem, the action of a group on a set, the Sylow theorems.
Two-dimensional vortex motion, and water waves
Graphs and subgraphs, trees
Existence theory, stability of linear and almost linear systems
Group-homomorphism, Group-Isomorphism, Group-Automorphism, Symmetric groups, Lagrange theorem, Quotient groups, Conjugation, p-groups and Sylow theory.
Normed spaces, Banach spaces, Hilbert spaces, Standard theorems.
Existence and uniqueness of solution of the first order ordinary differential equation, Linear system, Stability, First order quasi-linear partial differential equations, Cauchy problem.
(a) Basic equations, Inviscid Two-dimensional flow.
(b) Probability spaces, Mutually exclusive and independent events, Conditional probability, Discrete and continuous random variable, Density function, Distribution function, Expectation and variance, Some useful distribution function, Some useful inequalities, Generating functions and characteristic functions.
(b) Probability spaces, Mutually exclusive and independent events, Conditional probability, Discrete and continuous random variable, Density function, Distribution function, Expectation and variance, Some useful distribution function, Some useful inequalities, Generating functions and characteristic functions.
Rings, Ideals, Quotient rings, Ring Homomorphism, Commutative rings, Integral domains, Unique factorization domains, Field, Field extensions.
Linear Operators, Bounded Operators, Unbounded Operators, Spectral Theory.
Ordinary Differential Equation: Phase space Analysis, Existence Theory, Stability of Nonlinear System.
(a) Irrotational motion, Vortex Motion.
(b) Law of large numbers, Order in probability, Poisson process, Branching process, Birth and death process, Random walks.
(b) Law of large numbers, Order in probability, Poisson process, Branching process, Birth and death process, Random walks.
Frechet spaces, Locally convex spaces, Duality, Linear operators.
(a) Compact operators, Fredholm operators, Unbounded operators, Semigroup.
(a) Compact operators, Fredholm operators, Unbounded operators, Semigroup.
(a) Differential Equations and related topics: Theory of Elliptic, Parabolic and Hyperbolic Equations.
(b) Computational Mathematics: Numerical Linear Algebra
(b) Computational Mathematics: Numerical Linear Algebra
Viscous Motion: Viscous Incompressible Motion, Equation of Motion, Exact Solution.
(a) Introduction to mathematical statistics.
(b) Linear Programming: basic concepts, fundamental theorem of linear programming, simplex method, revised simplex method, duality theorem, complementary slackness theorem, sensitivity analysis, dual simplex method, primal dual algorithms, Integer Programming branch and bound algorithms, cutting plane methods.
(b) Linear Programming: basic concepts, fundamental theorem of linear programming, simplex method, revised simplex method, duality theorem, complementary slackness theorem, sensitivity analysis, dual simplex method, primal dual algorithms, Integer Programming branch and bound algorithms, cutting plane methods.